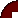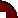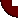Подходы к разработке языков моделирования.

К настоящему времени сложились два различных подхода к разработке языков моделирования: непрерывный и дискретный — отражающие основные особенности исследуемых методом моделирования систем. Поэтому ЯИМ делятся на две самостоятельные группы, которые соответствуют двум видам имитации, развивавшимся независимо друг от друга: для имитации непрерывных и дискретных процессов.

Для моделирования непрерывных процессов могут быть использованы не только АВМ, но и ЭВМ, последние при соответствующем программировании имитируют различные непрерывные процессы. При этом ЭВМ обладают большей надежностью в эксплуатации и позволяют получить высокую точность результатов, что привело к разработке языков моделирования, отображающих модель в виде блоков таких типов, которые играют роль стандартных блоков АВМ (усилителей, интеграторов, генераторов функций и т. п.).

Заданная схема моделирующего алгоритма преобразуется в систему совместно рассматриваемых дифференциальных уравнений. Моделирование в этом случае сводится, по сути дела, к отысканию численных решений этих уравнений при использовании некоторого стандартного пошагового метода.

Универсальная ЭВМ — устройство дискретного типа, а поэтому должна обеспечивать дискретную аппроксимацию процесса функционирования исследуемой системы S. Непрерывные изменения в процессе функционирования реальной системы отображаются в дискретной модели Ми, реализуемой на ЭВМ, некоторой последовательностью дискретных событий, и такие модели называются моделями дискретных событий. Отдельные события, отражаемые в дискретной модели, могут определяться с большой степенью приближения к действительности, что обеспечивает адекватность таких дискретных моделей реальным процессам, протекающим в системах S.

Архитектуру ЯИМ, т. е. концепцию взаимосвязей элементов языка как сложной системы, и технологию перехода от системы S к ее машинной модели Мы можно представить следующим образом:

1) объекты моделирования (системы S) описываются (отображаются в языке) с помощью некоторых атрибутов языка;

2) атрибуты взаимодействуют с процессами, адекватными реально протекающим явлениям в моделируемой системе S;  

3) процессы требуют конкретных условий, опреде¬ляющих логическую основу и последовательность взаимодействия этих процессов во времени;

4) условия влияют на события, имеющие место внутри объекта моделирования (системы S) и при взаимодействии с внешней средой Е;

5) события изменяют состояния модели системы М в пространстве и во времени.

В большинстве случаев с помощью машинных моделей исследуются характеристики и поведение системы S на определенном отрезке времени, поэтому одной из наиболее важных задач при создании модели системы и выборе языка программирования модели является реализация двух функций:

1) корректировка временной координаты состояния системы («продвижение» времени, организация «часов»);

2) обеспечение согласованности различных блоков и событий в системе (синхронизация во времени, координация с другими блоками).

Классификации языков моделирования

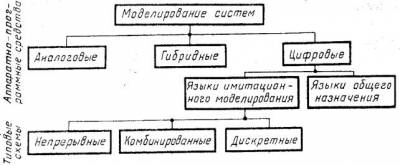
Для машинного моделирования системы S пригодны три способа проведения вычислений, в основе которых лежит применение цифровой, аналоговой и гибридной вычислительной техники рис. 1.

Для моделирования систем используются как универсальные и процедурно-ориентированные ЯОН, так и специализированные ЯИМ. При этом ЯОН предоставляют программисту-разработчику модели Мм больше возможностей в смысле гибкости разработки, отладки и использования модели. Но гибкость приобретается ценой больших усилий, затрачиваемых на программирование модели, так как организация выполнения операций, отсчет системного времени и контроль хода вычислений существенно усложняются.

Имеющиеся ЯИМ можно разбить на три основные группы, соответствующие трем типам математических схем: непрерывные, дискретные и комбинированные. Языки каждой группы предназначены для соответствующего представления системы S при создании ее машинной модели Мм.

В основе рассматриваемой классификации в некоторых ЯИМ лежит принцип формирования системного времени. Так как «системные часы» предназначены не только для продвижения системного времени в модели Мм, но также для синхронизации различных событий и операций в модели системы S, то при отнесении того или иного конкретного языка моделирования к определенному типу нельзя не считаться с типом механизма «системных часов».

Непрерывное представление системы S сводится к составлению уравнений, с помощью которых устанавливается связь между зависимыми и независимыми переменными модели. Примером такого непрерывного подхода является использование дифференциальных уравнений. Причем в дальнейшем дифференциальные уравнения могут быть применены для непосредственного получения характеристик системы.

Представление системы S в виде типовой схемы, в которой участвуют как непрерывные, так и дискретные величины, называется комбинированным. Состояние модели системы М(S) описывается набором переменных, некоторые из которых меняются во времени непрерывно. Законы изменения непрерывных компонент заложены в структуру, объединяющую дифференциальные уравнения и условия относительно переменных. Предполагается, что в системе могут наступать события двух типов:

1) события, зависящие от состояния системы;

2) события, зависящие от времени.

События первого типа наступают в результате выполнения условий, относящихся к законам изменения непрерывных переменных.

Для событий второго типа процесс моделирования состоит в продвижении системного времени от момента наступления события до следующего аналогичного момента.

В рамках дискретного подхода можно выделить несколько принципиально различных групп ЯИМ.

Первая группа ЯИМ подразумевает наличие списка событий, отличающих моменты начала выполнения операций. Продвижение времени осуществляется по событиям, в моменты наступления которых производятся необходимые операции, включая операции пополнения списка событий.

При использовании ЯИМ второй группы после пересчета системного времени, в отличие от схемы языка событий, просмотр действий с целью проверки выполнения условий начала или окончания какого-либо действия производится непрерывно. Просмотр действий определяет очередность появления событий.

Третья группа ЯИМ описывает системы, поведение которых определяется процессами. В данном случае под процессом понимается последовательность событий, связь между которыми устанавливается с помощью набора специальных отношений. Динамика заложена в независимо управляемых программах, которые в совокупности составляют программу процесса.